Module 1: Introduction to Neural Networks and Deep Learning

Deep Learning: Recent Advances and Applications

Deep learning has emerged as one of the most exciting fields in data science, with recent advancements leading to groundbreaking applications that were once considered nearly impossible. This note explores some of these remarkable applications and provides insights into why deep learning is currently experiencing such rapid growth.

Color Restoration

Color restoration is a fascinating application where grayscale images are automatically transformed into color. Researchers in Japan developed a system using Convolutional Neural Networks (CNNs) to achieve this. The system takes grayscale images and adds color to them, bringing them to life. This technology demonstrates the impressive capabilities of deep learning in image processing.

Speech Enactment

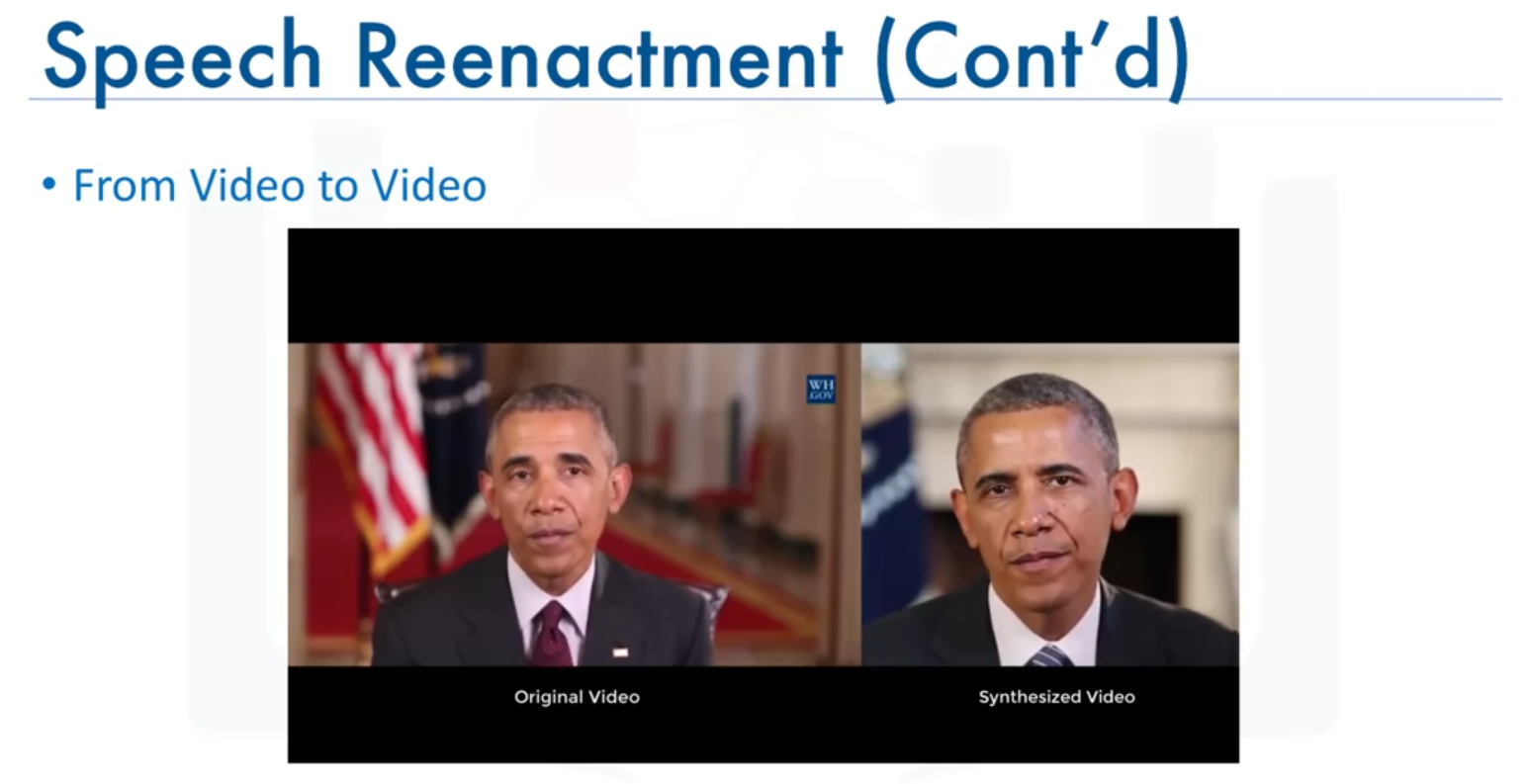
Speech enactment involves synthesizing audio clips with video and synchronizing lip movements with the spoken words. A notable advancement in this area was achieved by researchers at the University of Washington, who trained a Recurrent Neural Network (RNN) on a large dataset of video clips featuring a single person. Their system, demonstrated with a video of former President Barack Obama, produces realistic results where lip movements match the audio accurately.

The system can also extract audio from one video and sync it with lip movements in another, showcasing the versatility of this technology.

Automatic Handwriting Generation

Alex Graves from the University of Toronto designed an algorithm using RNNs for automatic handwriting generation. This algorithm can rewrite text in highly realistic cursive handwriting across various styles. Users can input text and either select a specific handwriting style or let the algorithm choose one randomly.

Other Applications

Deep learning encompasses a wide range of applications, including:

Automatic Machine Translation: Using CNNs to translate text in images in real-time.

Sound Addition to Silent Movies: Employing deep learning models to select appropriate sounds from a pre-recorded database to match scenes in silent films.

Object Classification and Self-Driving Cars: Classifying objects in images and enabling autonomous driving.

The Rise of Neural Networks

Despite the long history of neural networks, their recent surge in popularity can be attributed to advancements in technology and the availability of large datasets. These improvements have unlocked new possibilities and applications, making neural networks and deep learning more relevant than ever.

Summary

Deep learning has revolutionized numerous fields with its applications, from color restoration and speech enactment to handwriting generation and beyond. The continuous advancements in neural networks are driving these innovations and opening up new avenues for research and development.

Additional Notes: To fully grasp the potential of deep learning, further exploration into neural network specifics and deep learning techniques is essential.

Neural Networks: Biological Inspiration and Artificial Implementation

Deep learning algorithms draw inspiration from the way neurons and neural networks function in the human brain. Understanding this biological basis helps illuminate how artificial neural networks process information and learn.

Biological Neurons: Structure and Function

Neurons are the fundamental units of the brain, responsible for processing and transmitting information through electrical impulses. The study of neurons began with the pioneering work of Santiago Ramón y Cajal, who is considered the father of modern neuroscience.

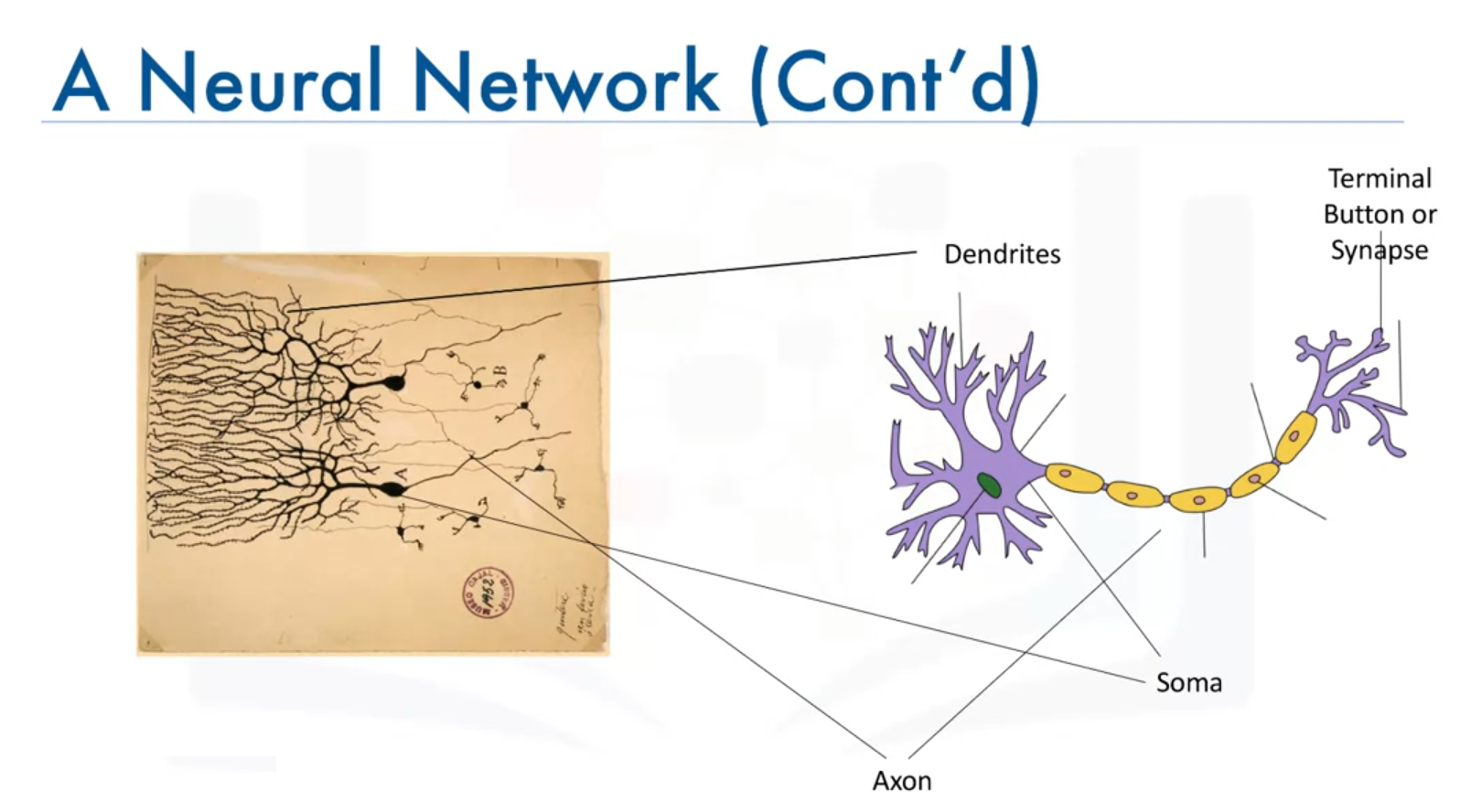
Structure of a Biological Neuron

Dendrites: Branch-like structures extending from the soma, responsible for receiving electrical impulses from other neurons.

Soma: The main body of the neuron, which contains the nucleus.

Axon: A long, slender projection that transmits electrical impulses away from the soma.

Synapses (Terminal Buttons): The endings of the axon, which pass the impulses (short electrical signals that carries information) to the dendrites of adjacent neurons.

Functioning of a Biological Neuron

Neurons receive electrical impulses through dendrites, process these impulses in the soma, and transmit the processed information through the axon to other neurons via synapses. Learning in the brain occurs by reinforcing certain neural connections through repeated activation, which strengthens these connections and makes them more likely to produce a desired outcome.

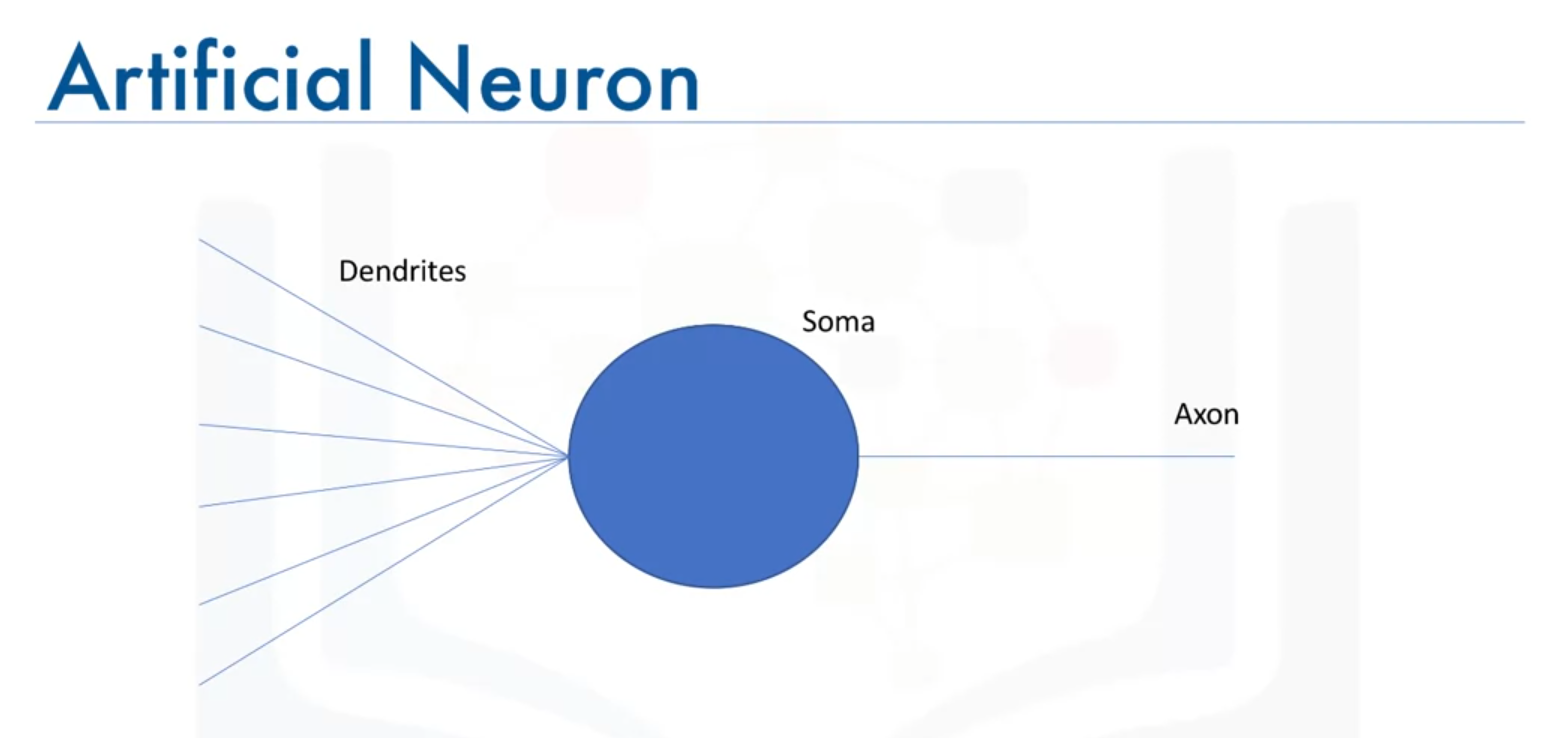
Artificial Neurons: Mimicking the Brain

Artificial neurons are modeled after biological neurons, incorporating similar components and processes:

Artificial Dendrites: Receive input data from other neurons.

Artificial Soma: Functions as the processing unit where inputs (analogous to electrical impulses) are combined.

Artificial Axon: Transmits the processed data to other neurons.

Artificial Synapse: The connection point where the output of one neuron becomes the input to another.

Learning in Artificial Neural Networks

The learning process in artificial neural networks closely resembles that of the brain. Through repeated activation and adjustment, the connections between artificial neurons are strengthened, enabling the network to produce more accurate outputs given specific inputs.

Summary

Neural networks, both biological and artificial, operate on the principle of processing inputs and transmitting outputs through interconnected neurons. The design of artificial neurons, inspired by the structure and function of biological neurons, allows deep learning models to emulate the learning processes of the human brain. Understanding this connection between biology and artificial intelligence provides a foundation for further exploration into the workings of neural networks.

Additional Notes: The detailed understanding of both biological and artificial neurons is essential for grasping the complexities of deep learning models and their applications. Further study on how these artificial systems learn and adapt will be covered in subsequent videos.

Mathematical Formulation of Neural Networks

Introduction

This note discusses the mathematical formulation of neural networks, focusing on the concepts of forward propagation, backpropagation, and activation functions. The emphasis here is on forward propagation, explained through a step-by-step example using numerical values.

Structure of a Neural Network

Neuron Resemblance

Artificial neurons are designed to resemble biological neurons.

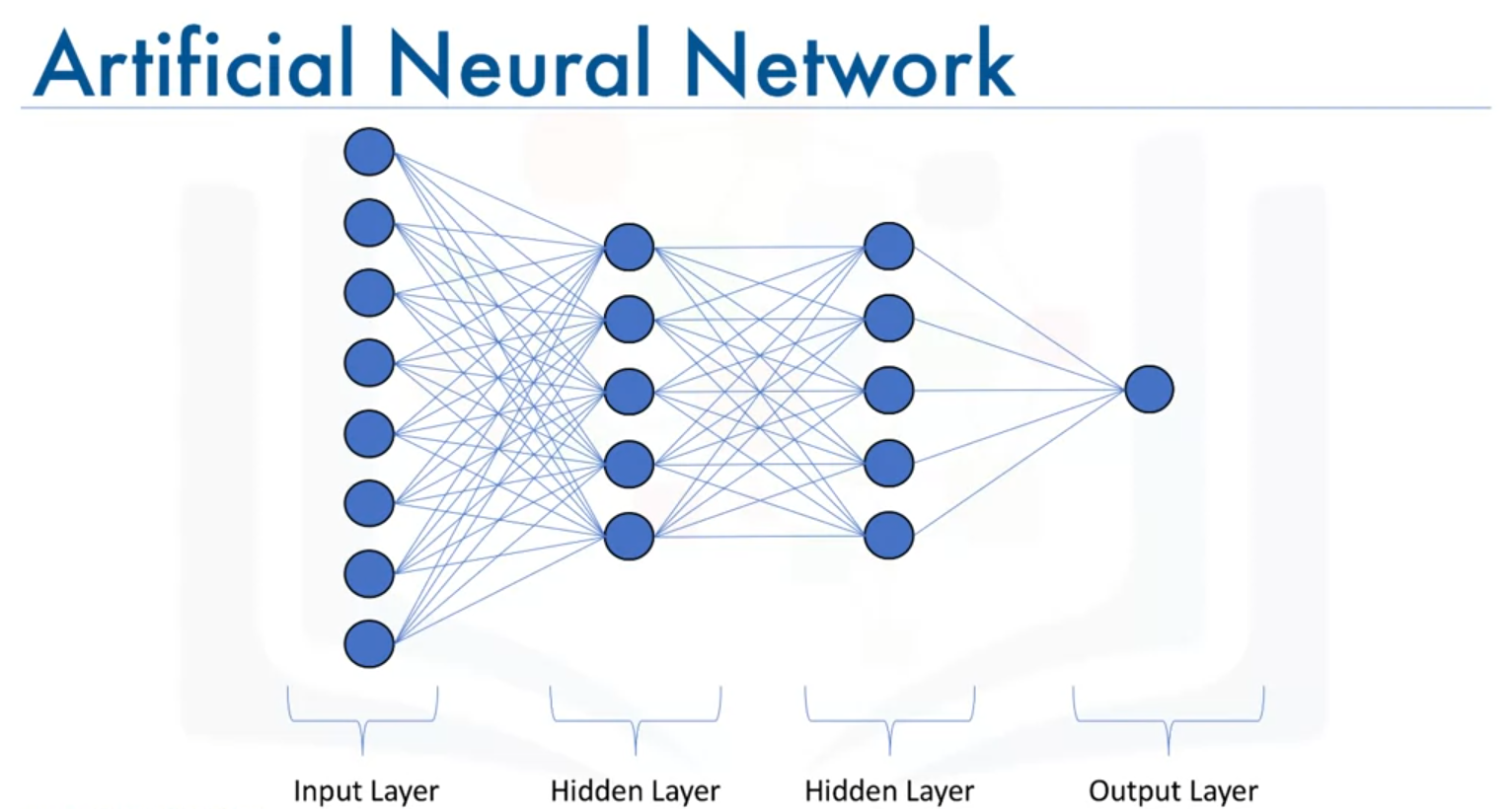
Layers in a Neural Network:
- Input Layer: The first layer that feeds input into the network.
- Output Layer: The final layer that provides the output of the network.
- Hidden Layers: Layers between the input and output layers.

Forward Propagation

Definition

Forward propagation is the process through which data passes through the layers of neurons in a neural network, moving from the input layer to the output layer.

Mathematical Formulation

Single Neuron Example

Consider a neuron with two inputs, $x_1$ and $x_2$ , and corresponding weights $w_1$ and $w_2$ . The neuron computes a weighted sum of the inputs and adds a bias term $b$ to produce an output.

Mathematical Expression:

z = w_1 \cdot x_1 + w_2 \cdot x_2 + b

The output of the neuron, $a$ , is the result of applying an activation function to $z$ .

a = \sigma(z)

where $\sigma(z)$ is the sigmoid activation function.

Example Calculation

Given the following values:

$x_1 = 0.1$

$w_1 = 0.15$

$b_1 = 0.4$

Step 1: Compute $z$

z = w_1 \cdot x_1 + b_1 = 0.15 \cdot 0.1 + 0.4 = 0.415

Step 2: Apply Sigmoid Function

\sigma(z) = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-0.415}} \approx 0.6023

Multiple Neurons Example

For a network with two neurons:

The output from the first neuron, $a_1=0.6023$ , becomes the input to the second neuron.

Given $w_2$ and $b_2$ , the output of the second neuron is computed in the same way.

Example Calculation for the Second Neuron

Given:

$w_2 = 0.25$

$b_2 = 0.5$

Step 1: Compute $z_2$

z_2 = w_2 \cdot a_1 + b_2 = 0.25 \cdot 0.6023 + 0.5 = 0.6506

Step 2: Apply Sigmoid Function

a_2 = \sigma(z_2) \approx 0.7153

This is the predicted output for the given input.

Activation Functions

Importance

Activation functions introduce non-linearity into the network, enabling it to learn and perform complex tasks.

Without an activation function, a neural network behaves like a linear regression model and can only make straight-line predictions because it combines inputs in a simple, linear way. This limits the network to solving problems where the relationship between inputs and outputs is straightforward. An activation function adds the ability to capture more complex, curved patterns, making the network capable of handling more complicated tasks.

Sigmoid Function

The sigmoid function is commonly used as an activation function.

It maps any real-valued number into a value between 0 and 1.

It helps to decide whether a neuron should be activated (closer to 1) or not (closer to 0), allowing the network to handle complex patterns and make decisions.

\sigma(z) = \frac{1}{1 + e^{-z}}

Summary

Forward propagation involves computing the weighted sum of inputs, adding a bias, and applying an activation function to generate an output.

This process is repeated for each neuron in the network.

The final output of the network is obtained by propagating data through all the layers.

Key Points

Input Layer: Feeds data into the network.

Hidden Layers: Process data using weights, biases, and activation functions.

Output Layer: Produces the final prediction.

Additional Notes:

Forward propagation is like passing information through a neural network to make a prediction. It starts with the input data, moves through the network's layers (where each layer processes the data a bit more), and ends with an output or prediction.

Backward propagation is the process of improving the network by learning from its mistakes. After making a prediction, the network checks how far off it was from the correct answer, then goes back through the layers and adjusts the connections (weights and biases) to make better predictions in the future. This process is repeated many times to help the network learn.